On September 9th, 1990, Marilyn Vos Savant, regarded as the most intelligent person at the time with a record IQ of 228, received a question about a theoretical gameshow scenario, similar to the situations depicted in Let’s Make A Deal, hosted by the famous Monty Hall. The question is as follows:
“The problem posed is that you have three closed doors, behind one of which is a car, and behind the other two are goats. You get to pick one of the closed doors, and will win whatever is behind it (you want the car).
One of the doors you did not pick is now opened, revealing a goat. You therefore now know the car is either behind the door you picked or behind the other closed door.
In this setup, the question is: if offered the chance to switch your selection from the door you initially picked to the other closed door, should you switch? Does it make a difference?“
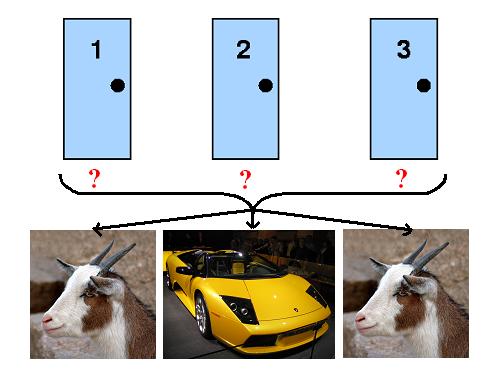
Let’s visualize the question. Behind one of the doors, there is a car. The other two doors contain goats. Your goal is to find the door which has the car behind it.
You choose door #1 as your pick. Monty Hall, who is the supposed host for this show, opens door #2, which contains a goat. Monty Hall gives you the choice to switch the door you chose, which is door #1, for the remaining door, which is door #3.
Should you take the opportunity to switch your choice to door #3 or should you stick with door #1?
The answer seems obvious. You are left with two doors, one with the car and one with the goat, so there should be a 50% chance that you get it correct. It shouldn’t matter at all whether you switch or stick, right? But, that is not the entire answer.
Why is the Chance not 50%?

The key to this problem is not to imagine each door having a 1/3 chance of getting the car, but instead to imagine that the door you chose to have a 1/3 chance and to group the two doors you didn’t choose with a 2/3 chance. This groups the doors you didn’t choose together into one singular probability.
When Monty Hall opens door #2 to reveal a goat, it is important to realize that door #3 actually receives all of the 2/3 probability. This pits your 1/3 chance of door #1 having the car against the 2/3 chance of door #3 having the car.
The 2/3 chance that was grouped before door #2 was revealed to have a goat has to go somewhere. It cannot be split into two 1/3 chances between doors #2 and #3 because door #2 has a goat behind the door.
Conclusion
If you are given the chance to switch doors in a Monty Hall type situation, then you should switch doors. This is because 2/3 chance that one of the doors that you didn’t choose has the car behind it cannot magically form into both remaining doors having a 50% chance. That 2/3 chance has to go somewhere, and so it goes to the other remaining door that you didn’t choose.
Related Stories:
- https://betterexplained.com/articles/
- understanding-the-monty-hall-problem/
- https://www.montyhallproblem.com/
- https://mathworld.wolfram.com/MontyHallProblem.html
- https://medium.com/@ProfessorF/visualizing-the-solution-to-the-monty-hall-problem-bf4a08c8ed8f
- https://www.statisticshowto.com/probability-and-statistics/monty-hall-problem/
Take Action: